barter2016metafoodchains
Meta-food-chains as a many-layer epidemic process on networks
Edmund Barter and Thilo Gross
Phys. Rev. E 93, 022303, 2016
Notable recent works have focused on the multi-layer properties of coevolving diseases. We point out that very similar systems play an important role in population ecology. Specifically we study a meta food-web model that was recently proposed by Pillai et al. This model describes a network of species connected by feeding interactions, which spread over a network of spatial patches. Focusing on the essential case, where the network of feeding interactions is a chain, we develop an analytical approach for the computation of the degree distributions of colonized spatial patches for the different species in the chain. This framework allows us to address ecologically relevant questions. Considering configuration model ensembles of spatial networks, we find that there is an upper bound for the fraction of patches that a given species can occupy, which depends only on the networks mean degree. For a given mean degree there is then an optimal degree distribution that comes closest to the upper bound. Notably scale-free degree distributions perform worse than more homogeneous degree distributions if the mean degree is sufficiently high. Because species experience the underlying network differently the optimal degree distribution for one particular species is generally not the optimal distribution for the other species in the same food web. These results are of interest for conservation ecology, where, for instance, the task of selecting areas of old-growth forest to preserve in an agricultural landscape, amounts to the design of a patch network.
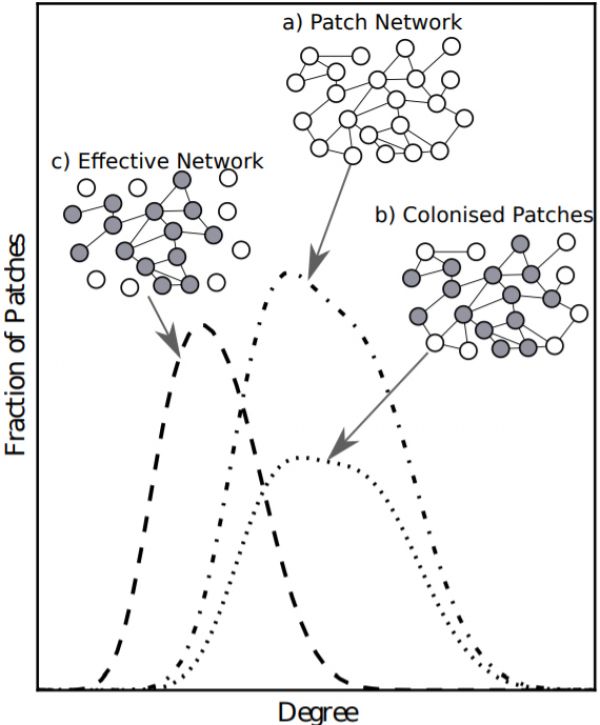
Figure 1: Example of the two step process for finding the degree distribution of the effective network of species 2. We start
with the patch network and its degree distribution, \(p_k\), (a). The first step identifies the nodes colonised by the species, \(\xi_k\), (b). The second step removes links from colonised nodes to uncolonised nodes from the distribution giving the effective network, \(g_k\), (c). This is the network upon which species 2 disperses.