baurmann2007instabilities
Instabilities in spatially extended predator–prey systems: Spatio-temporal patterns in the neighborhood of Turing–Hopf bifurcations
Martin Baurmann, Thilo Gross and Ulrike Feudel
Journal of Theoretical Biology 245, 220-229, 2007
We investigate the emergence of spatio-temporal patterns in ecological systems. In particular, we study a generalized predator–prey system on a spatial domain. On this domain diffusion is considered as the principal process of motion. We derive the conditions for Hopf and Turing instabilities without specifying the predator–prey functional responses and discuss their biological implications. Furthermore, we identify the codimension-2 Turing–Hopf bifurcation and the codimension-3 Turing–Takens–Bogdanov bifurcation. These bifurcations give rise to complex pattern formation processes in their neighborhood. Our theoretical findings are illustrated with a specific model. In simulations a large variety of different types of long-term behavior, including homogenous distributions, stationary spatial patterns and complex spatio-temporal patterns, are observed.
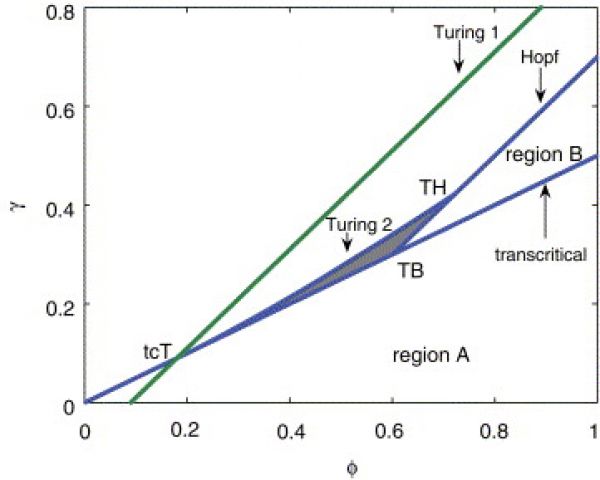
Figure 1: The bifurcation diagram shows the Turing space as the grey triangular area bounded by the Turing bifurcation, the Hopf bifurcation and the transcritical bifurcation. The whole parameter space above transcritical and Hopf bifurcation with exception of the Turing space corresponds to unconditionally stable equilibria.