BioND | Hunting French ducks in a noisy environment

Abstract Citation export ArXiv preprint Publisher's page

berglund2012hunting

Hunting French ducks in a noisy environment

Nils Berglund, Barbara Gentz and Christian Kuehn

Journal of Differential Equations 252, 4786-4841, 2012

We consider the effect of Gaussian white noise on fast-slow dynamical systems with one fast and two slow variables, containing a folded-node singularity. In the absence of noise, these systems are known to display mixed-mode oscillations, consisting of alternating large- and small-amplitude oscillations. We quantify the effect of noise and obtain critical noise intensities above which the small-amplitude oscillations become hidden by fluctuations. Furthermore we prove that the noise can cause sample paths to jump away from so-called canard solutions with high probability before deterministic orbits do. This early-jump mechanism can drastically influence the local and global dynamics of the system by changing the mixed-mode patterns.

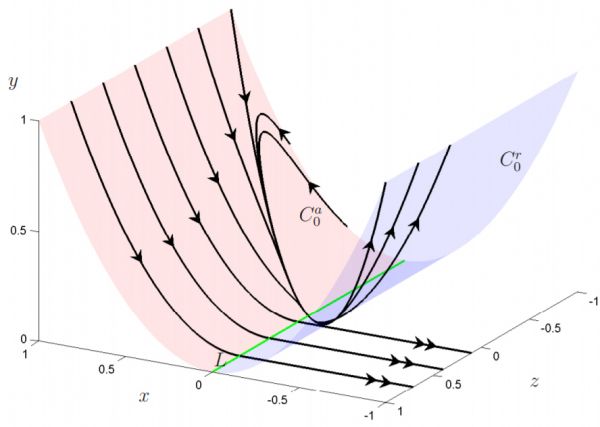
$Singular limit $\epsilon = 0$ for the normal form (3.8) with $\mu = 0.15$. The attracting manifold $C_0^a$ (red), the fold line $L$ (green) and the repelling manifold $C_0^r$ (blue) partition the critical manifold. Trajectories of the slow (fast) subsystem are indicated by single (double) arrows.$

Figure 1: Singular limit $\epsilon = 0$ for the normal form (3.8) with $\mu = 0.15$. The attracting manifold $C_0^a$ (red), the fold line $L$ (green) and the repelling manifold $C_0^r$ (blue) partition the critical manifold. Trajectories of the slow (fast) subsystem are indicated by single (double) arrows.