bohme2013emergence
Emergence and persistence of diversity in complex networks
Complex networks are employed as a mathematical description of complex systems in many different fields, ranging from biology to sociology, economy and ecology. Dynamical processes in these systems often display phase transitions, where the dynamics of the system changes qualitatively. In combination with these phase transitions certain components of the system might irretrievably go extinct. In this case, we talk about absorbing transitions. Developing mathematical tools, which allow for an analysis and prediction of the observed phase transitions is crucial for the investigation of complex networks. In this article we address absorbing transitions in dynamical networks, where a certain amount of diversity is lost. In some real-world examples, e.g. in the evolution of human societies or of ecological systems, it is desirable to maintain a high degree of diversity, whereas in others, e.g. in epidemic spreading, the diversity of diseases is worthwhile to confine. An understanding of the underlying mechanisms for emergence and persistence of diversity in complex systems is therefore essential. Within the scope of two different network models, we develop an analytical approach, which can be used to estimate the prerequisites for diversity. The mathematical framework presented here is based on concepts from percolation theory. While the specific implementation of the formalism differs from model to model, the basic principle allows for the calculation of absorbing phase transitions in a wide range of different network models.
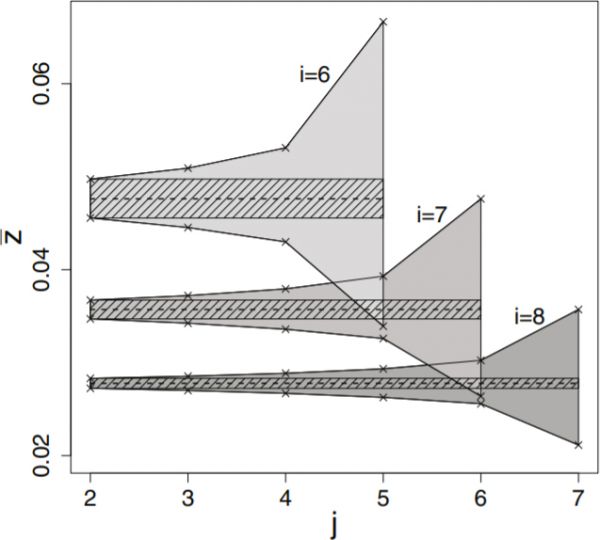
Figure 1: Coexistence range for an omnivore in dependence on the trophic levels of its prey species. The grey regions show the coexistence ranges for different values of \(i\) and varying \(j\), corresponding to the formulae given in (4.17). The coexistence range becomes smaller with increasing \(i\) and with decreasing \(j\) (for fixed \(i\)). Dashed lines indicate the respective invasion thresholds of species \(i\). The dashed region marks the parameter range where most omnivores are able to coexist with the specialist chain. The maximal number of coexisting omnivores for a given chain of length \(i\) yields \(n_{\rm max} = i − 1\).
