BioND | All scale-free networks are sparse

Abstract Coverage Citation export ArXiv preprint Publisher's page

delgenio2011all

All scale-free networks are sparse

Charo I. Del Genio, Thilo Gross and Kevin E. Bassler

Phys. Rev. Lett. 107, 178701, 2011

We study the realizability of scale free-networks with a given degree sequence, showing that the fraction of realizable sequences undergoes two first-order transitions at the values 0 and 2 of the power-law exponent. We substantiate this finding by analytical reasoning and by a numerical method, proposed here, based on extreme value arguments, which can be applied to any given degree distribution. Our results reveal a fundamental reason why large scale-free networks without constraints on minimum and maximum degree must be sparse.

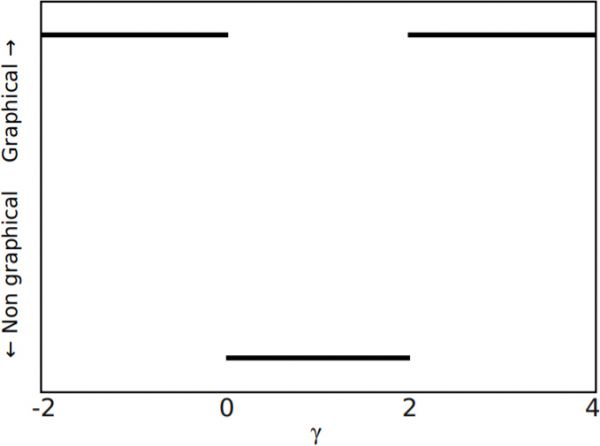
$Graphicality of the degree maximizing sequence ($N = 10^6$) given by Eq. 11 for scale-free distributions vs. exponent $\gamma$. The graphicality transitions points are correctly identified.$

Figure 1: Graphicality of the degree maximizing sequence ($N = 10^6$) given by Eq. 11 for scale-free distributions vs. exponent $\gamma$. The graphicality transitions points are correctly identified.

"Few and far between"

Commentary by Sitabhra Sinha, Physics, Oct 17, 2011