BioND | Emergent bipartiteness in a society of knights and knaves

Abstract Citation export ArXiv preprint Publisher's page

delgenio2011emergent

Emergent bipartiteness in a society of knights and knaves

C I Del Genio and T Gross

New J. Phys. 13, 103038, 2011

We propose a simple model of a social network based on so-called knights-and-knaves puzzles. The model describes the formation of networks between two classes of agents where links are formed by agents introducing their neighbours to others of their own class. We show that if the proportion of knights and knaves is within a certain range, the network self-organizes to a perfectly bipartite state. However, if the excess of one of the two classes is greater than a threshold value, bipartiteness is not observed. We offer a detailed theoretical analysis for the behaviour of the model, investigate its behaviou r in the thermodynamic limit, and argue that it provides a simple example of a topology-driven model whose behaviour is strongly reminiscent of a first-order phase transitions far from equilibrium.

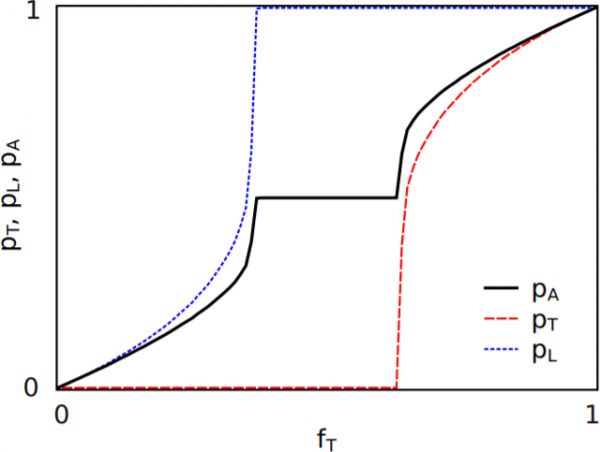
$Emergent bipartiteness. Ensemble averaged probabilities for a neighbour of a knight to be a knight ($p_T$, dashed red line), for a neighbour of a knave to be a knight ($p_L$, dotted blue line), and for a neighbour of any node to be a knight ($p_A$, solid black line), as a function of the fraction $f_T$ of knights in the network. The lines are averages over an ensemble of $10^4$ networks with $N = 10^4$ nodes.$

Figure 1: Emergent bipartiteness. Ensemble averaged probabilities for a neighbour of a knight to be a knight ($p_T$, dashed red line), for a neighbour of a knave to be a knight ($p_L$, dotted blue line), and for a neighbour of any node to be a knight ($p_A$, solid black line), as a function of the fraction $f_T$ of knights in the network. The lines are averages over an ensemble of $10^4$ networks with $N = 10^4$ nodes.