demirel2011cyclic
Cyclic dominance in adaptive networks
G. Demirel, R. Prizak, P. N. Reddy and T. Gross
Eur. Phys. J. B 84, 541-548, 2011
The Rock-Paper-Scissors(RPS) game is a paradigmatic model for cyclic dominance in biological systems. Here we consider this game in the social context of competition between opinions in a networked society. In our model, every agent has an opinion which is drawn from the three choices: rock, paper or scissors. In every timestep a link is selected randomly and the game is played between the nodes connected by the link. The loser either adopts the opinion of the winner or rewires the link. These rules define an adaptive network on which the agent's opinions coevolve with the network topology of social contacts. We show analytically and numerically that nonequilibrium phase transitions occur as a function of the rewiring strength. The transitions separate four distinct phases which differ in the observed dynamics of opinions and topology. In particular, there is one phase where the population settles to an arbitrary consensus opinion. We present a detailed analysis of the corresponding transitions revealing an apparently paradoxial behavior. The system approaches consensus states where they are unstable, whereas other dynamics prevail when the consensus states are stable.
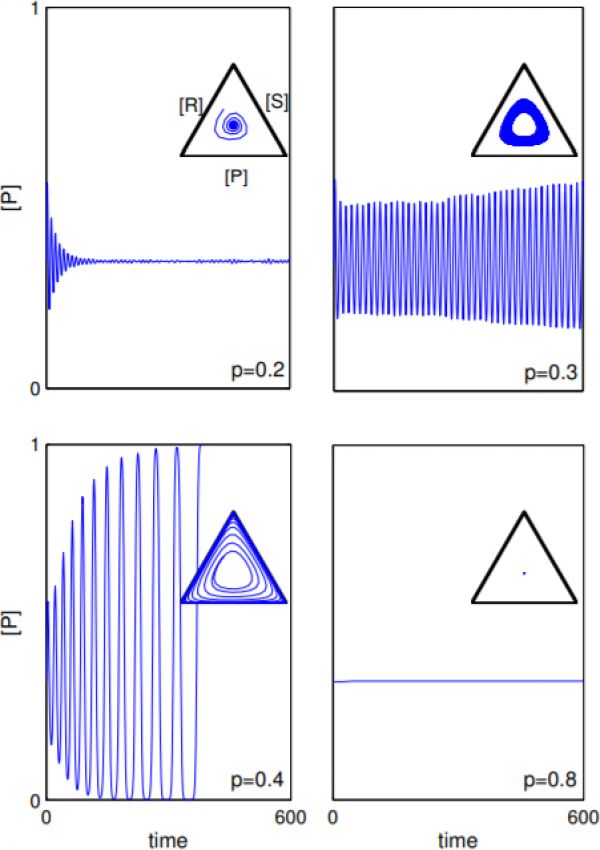
Figure 1: Transient and long term dynamics of the RPS system. The timeseries show the density of players holding the opinion P in four different phases: stationary phase (top-left, \(p = 0.2\)), oscillatory phase (top-right, \(p = 0.3\)), consensus phase (bottom-left, \(p = 0.4\)), and fragmented phase (bottom-right, \(p = 0.8\)) The insets show the corresponding long-term
behavior in the ternary phase space spanned by the opinion densities R, P, and S.