do2012engineering
Engineering mesoscale structures with distinct dynamical implications
The dynamics of networks of interacting systems depends intricately on the interaction topology. When the dynamics is explored, generally the whole topology has to be considered. However, we show that there are certain mesoscale subgraphs that have precise and distinct consequences for the system-level dynamics. In particular, if meso-scale symmetries are present then eigenvectors of the Jacobian localise on the symmetric subgraph and the corresponding eigenvalues become insensitive to the topology outside the subgraph. Hence, dynamical instabilities associated with these eigenvalues can be analyzed without considering the topology outside the subgraph. While such instabilities are thus generated entirely in small network subgraphs, they generally do not remain confined to the subgraph once the instability sets in and thus have system-level consequences. Here we illustrate the analytical investigation of such instabilities in an ecological meta-population model consisting of a network of delay-coupled delay oscillators.
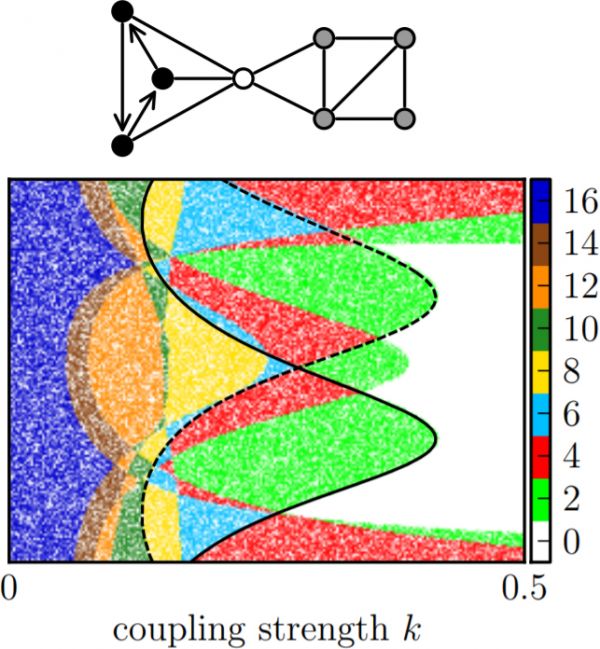
Figure 1: Characteristic instabilities induced by the directed triangle subgraph. The scatter plot shows the stability of specific pairs of the parameters \((k, \delta)\). Color-coded is the number of dynamical eigenvalues with positive real parts, such that white corresponds to the region where the homogeneous steady state is stable. The solid and dashed lines
correspond to analytical results for bifurcations that are localised in the triangle subgraph. The agreement between the scatter plot and the analytically obtained bifurcation lines show that the bifurcation lines of the two localised eigenvalues of the BSS are not affected by the residual graph.