gross2006epidemic
Epidemic Dynamics on an Adaptive Network
Many real world networks are characterized by adaptive changes in their topology depending on the dynamic state of their nodes. Here we study epidemic dynamics in an adaptive network, where susceptibles are able to avoid contact with infected by rewiring their network connections. We demonstrate that adaptive rewiring has profound consequences for the emerging network structure, giving rise to assortative degree correlation and a separation into two loosely connected sub-compartments. This leads to dynamics such as oscillations, hysteresis and 1st order transitions. We describe the system in terms of a simple model using a pair-approximation and present a full local bifurcation analysis. Our results indicate that the interplay between dynamics and topology can have important consequences for the spreading of infectious diseases and related applications.
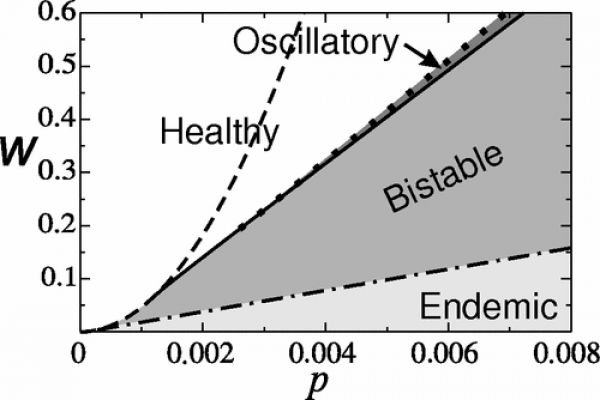
Figure 1: Two parameter bifurcation diagram showing the dependence on the rewiring rate \(w\) and the infection probability \(p\). In the white and light gray regions there is only a single attractor, which is a healthy state in the white region and an endemic state in the light gray region. In the medium gray region both of these states are stable. Another smaller region of bistability is shown in dark gray. Here, a stable healthy state coexists with a stable epidemic cycle. The transition lines between these regions correspond to transcritical (dash-dotted), saddle-node (dashed), Hopf (continuous), and cycle fold (dotted) bifurcations.