hofener2011stability
Stability of networks of delay-coupled delay oscillators
J. M. Höfener, G. C. Sethia and T. Gross
EPL 95, 40002, 2011
Dynamical networks with time delays can pose a considerable challenge for mathematical analysis. Here, we extend the approach of generalized modeling to investigate the stability of large networks of delay-coupled delay oscillators. When the local dynamical stability of the network is plotted as a function of the two delays then a pattern of tongues is revealed. Exploiting a link between structure and dynamics, we identify conditions under which perturbations of the topology have a strong impact on the stability. If these critical regions are avoided the local stability of large random networks can be well approximated analytically.
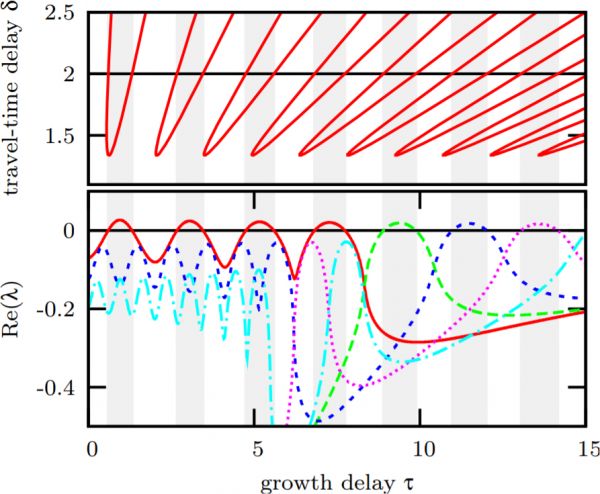
Figure 1: Lattice symmetry in the bifurcation points. Top: Blowup of a part of the bifurcation diagram. Bottom: Selected eigenvalues of the Jacobian (different colors) along a one dimensional cut at \(\delta=2\) (black line, top). Shaded regions mark values of \(\tau\) where the system with \(\delta=2\) is unstable.