kuehn2011decomposing
On decomposing mixed-mode oscillations and their return maps
Christian Kuehn
Chaos 21, 033107, 2011
Alternating patterns of small and large amplitude oscillations occur in a wide variety of physical, chemical, biological and engineering systems. These mixed-mode oscillations (MMOs) are often found in systems with multiple time scales. Previous differential equation modeling and analysis of MMOs has mainly focused on local mechanisms to explain the small oscillations. Numerical continuation studies reported different MMO patterns based on parameter variation. This paper aims at improving the link between local analysis and numerical simulation. Our starting point is a numerical study of a singular return map for the Koper model which is a prototypical example for MMOs that also relates to local normal form theory. We demonstrate that many MMO patterns can be understood geometrically by approximating the singular maps with affine and quadratic maps. Motivated by our numerical analysis we use abstract affine and quadratic return map models in combination with two local normal forms that generate small oscillations. Using this decomposition approach we can reproduce many classical MMO patterns and effectively decouple bifurcation parameters for local and global parts of the flow. The overall strategy we employ provides an alternative technique for understanding MMOs.
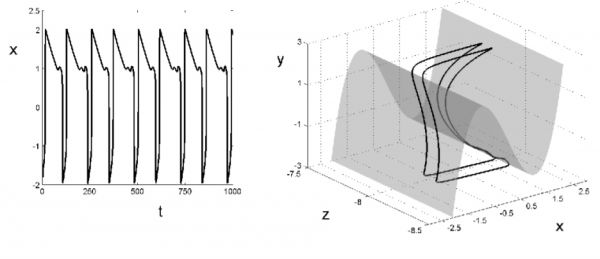
Figure 1: Example of a mixed-mode oscllation.