meisel2009adaptive
Adaptive self-organization in a realistic neural network model
Christian Meisel and Thilo Gross
Phys. Rev. E 80, 061917, 2009
Information processing in complex systems is often found to be maximally efficient close to critical states associated with phase transitions. It is therefore conceivable that also neural information processing operates close to criticality. This is further supported by the observation of power-law distributions, which are a hallmark of phase transitions. An important open question is how neural networks could remain close to a critical point while undergoing a continual change in the course of development, adaptation, learning, and more. An influential contribution was made by Bornholdt and Rohlf, introducing a generic mechanism of robust self-organized criticality in adaptive networks. Here, we address the question whether this mechanism is relevant for real neural networks. We show in a realistic model that spike-time-dependent synaptic plasticity can self-organize neural networks robustly toward criticality. Our model reproduces several empirical observations and makes testable predictions on the distribution of synaptic strength, relating them to the critical state of the network. These results suggest that the interplay between dynamics and topology may be essential for neural information processing.
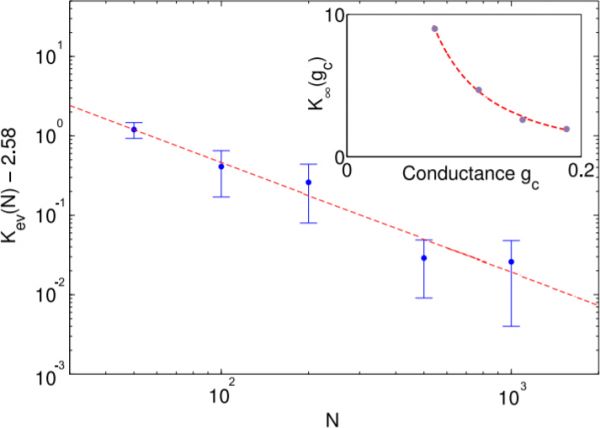
Figure 1: Scaling of the self-organized connectivity. The final value of connectivity approached in simulation follows a power-law depending on the number of neurons \(N\) and synaptic conductances \(g_c\) (inset). The values shown were
found by averaging over 30000 iterations and 3 estimates of the connectivity \(K_\infty\).