stiefs2009evidence
Evidence of chaos in eco-epidemic models
We study an eco-epidemic model with two trophic levels in which the dynamics are determined by predator-prey interactions as well as the vulnerability of the predator to a disease. Using the concept of generalized models we show that for certain classes of eco-epidemic models quasiperiodic and chaotic dynamics are generic and likely to occur. This result is based on the existence of bifurcations of higher codimension such as double Hopf bifurcations. We illustrate the emergence of chaotic behavior with one example system.
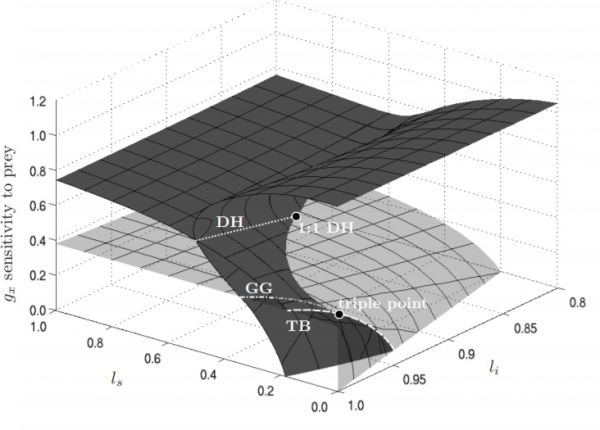
Figure 1: Bifurcation diagram of the generalized eco-epidemic model. A surface of Hopf bifurcations (dark) and a surface of
saddle-node type bifurcations (transparent bright) are shown. The intersection lines are a Takens-Bogdanov bifurcation line (TB), a Gavrilov-Guckenheimer bifurcation line (GG), and a double-Hopf bifurcation line (DH). The double-Hopf bifurcation line ends in a 1:1 resonant double-Hopf bifurcation point (1:1 DH) and the Gavrilov-Guckenheimer bifurcation line ends in a triple point bifurcation at the Takens-Bogdanov line. The bifurcation parameters are the generalized parameters \(g_x\), \(l_s\) and \(l_i\) , which are strongly related to the functional form of the underlying processes, namely the per capita functional response \(g(x)\) and the incidence function \(l(y_s, y_i)\) respectively.