vanvoorn2008stabilization
Stabilization due to predator interference: comparison of different analysis approaches
George A. K. van Voorn, Dirk Stiefs, Thilo Gross, Bob W. Kooi, Ulrike Feudel and Sebastiaan A. L. M. Kooijman
Mathematical Biosciences and Engineering 5, 567-583, 2008
We study the influence of the particular form of the functional response in two-dimensional predator-prey models with respect to the stability of the non-trivial equilibrium. This equilibrium is stable between its appearance at a transcritical bifurcation and its destabilization at a Hopf bifurcation giving rise to periodic behavior. Based on local bifurcation analysis we introduce a classification of stabilizing effects. The classical Rosenzweig-MacArthur model can be classified as weakly stabilizing, undergoing the paradox of enrichment, while the well-known Beddington-DeAngelis model can be classified as strongly stabilizing. Under certain conditions we obtain a complete stabilization resulting in an avoidance of limit cycles. Both models, in their
conventional formulation, are compared to a generalized, steady-state independent two-dimensional version of these models, based on a previously developed normalization method. We show explicitly how conventional and generalized models are related and how to interpret the results from the rather abstract stability analysis of generalized models.
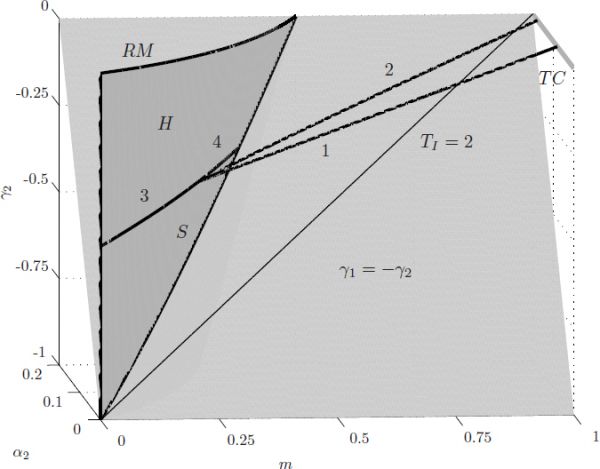
Figure 1: Three-dimensional bifurcation diagram of the Beddington-DeAngelis model.