bohme2011analytical
Analytical calculation of fragmentation transitions in adaptive networks
Gesa A. Böhme and Thilo Gross
Phys. Rev. E 83, 035101, 2011
In adaptive networks fragmentation transitions have been observed in which the network breaks into disconnected components. We present an analytical approach for calculating the transition point in general adaptive network models. Using the example of an adaptive voter model, we demonstrate that the proposed approach yields good agreement with numerical results.
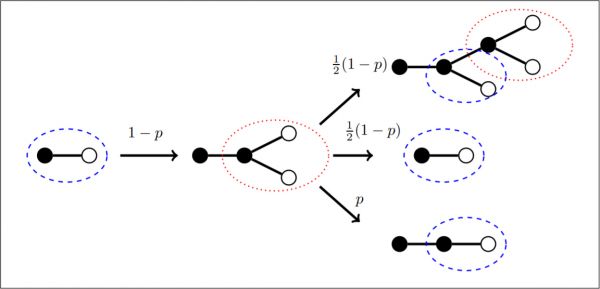
Figure 1: Illustration of the evolution of active links in a degree regular network with degree \(k = 3\). Agents are depicted as nodes which are open or solid depending on their opinion. Shown is the network in the neighborhood of an active link connecting nodes of different opinions. Arrows correspond to dynamical updates and are labeled with the corresponding transition rate. Depending on the parameters the updates lead to proliferation or decline of isolated active links (encircled dotted) and 2-fan motifs (encircled dashed).