silk2014exploring
Exploring the adaptive voter model dynamics with a mathematical triple jump
Holly Silk, Güven Demirel, Martin Homer and Thilo Gross
New J. Phys. 16, 093051, 2014
Progress in theoretical physics is often made by the investigation of toy models, the model organisms of physics, which provide benchmarks for new methodologies. For complex systems, one such model is the adaptive voter model. Despite its simplicity, the model is hard to analyse. Only inaccurate results are obtained from well-established approximation schemes that work well on closely-related models. We use this model to illustrate a new approach that combines a) the use of a heterogeneous moment expansion to approximate the network model by an infinite system of ordinary differential equations, b) generating functions to map the ordinary differential equation system to a two-dimensional partial differential equation, and c) solution of this partial differential equation by the tools of PDE-theory. Beyond the adaptive voter models, the proposed approach establishes a connection between network science and the theory of partial differential equations and is widely applicable to the dynamics of networks with discrete node-states.
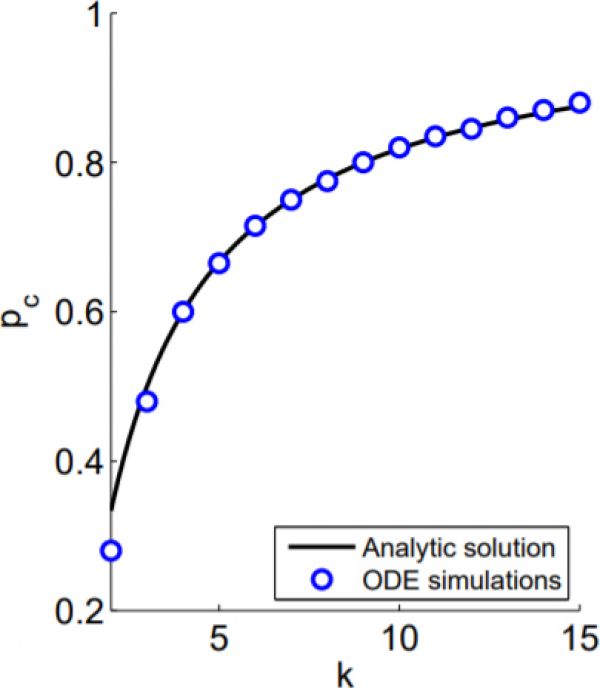
Figure 1: Fragmentation transition in a large ODE simulation compared to the analytical solution.