brechtel2018master
Master stability functions reveal diffusion-driven pattern formation in networks
Andreas Brechtel, Philipp Gramlich, Daniel Ritterskamp, Barbara Drossel and Thilo Gross
Phys. Rev. E 97, 032307, 2018
We study diffusion-driven pattern-formation in networks of networks, a class of multilayer systems, where different layers have the same topology, but different internal dynamics. Agents are assumed to disperse within a layer by undergoing random walks, while they can be created or destroyed by reactions between or within a layer. We show that the stability of homogeneous steady states can be analyzed with a master stability function approach that reveals a deep analogy between pattern formation in networks and pattern formation in continuous space.For illustration we consider a generalized model of ecological meta-foodwebs. This fairly complex model describes the dispersal of many different species across a region consisting of a network of individual habitats while subject to realistic, nonlinear predator-prey interactions. In this example the method reveals the intricate dependence of the dynamics on the spatial structure. The ability of the proposed approach to deal with this fairly complex system highlights it as a promising tool for ecology and other applications.
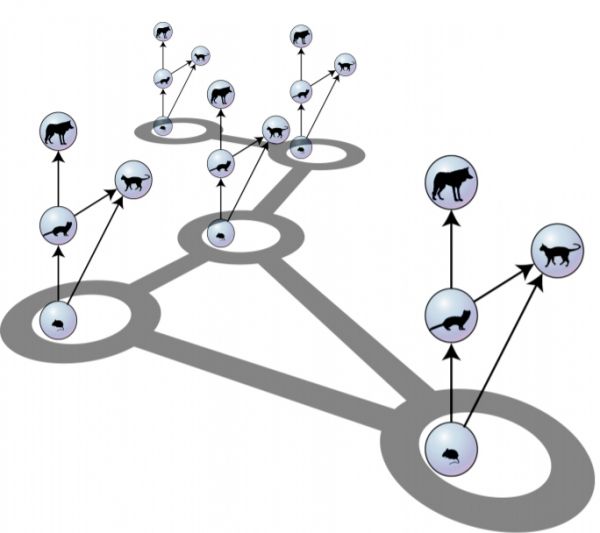
Figure 1: Illustration of a meta-foodweb as a multiplex network.