kuehn2013nonlocal
Nonlocal generalized models of predator-prey systems
Christian Kuehn and Thilo Gross
Discrete & Continuous Dynamical Systems - B 18, 693-720, 2013
The method of generalized modeling has been applied successfully in many different contexts, particularly in ecology and systems biology. It can be used to analyze the stability and bifurcations of steady-state solutions. Although many dynamical systems in mathematical biology exhibit steady-state behaviour one also wants to understand nonlocal dynamics beyond equilibrium points. In this paper we analyze predator-prey dynamical systems and extend the method of generalized models to periodic solutions. First, we adapt the equilibrium generalized modeling approach and compute the unique Floquet multiplier of the periodic solution which depends upon so-called generalized elasticity and scale functions. We prove that these functions also have to satisfy a flow on parameter (or moduli) space. Then we use Fourier analysis to provide computable conditions for stability and the moduli space flow. The final stability analysis reduces to two discrete convolutions which can be interpreted to understand when the predator-prey system is stable and what factors enhance or prohibit stable oscillatory behaviour. Finally, we provide a sampling algorithm for parameter space based on nonlinear optimization and the Fast Fourier Transform which enables us to gain a statistical understanding of the stability properties of periodic predator-prey dynamics.
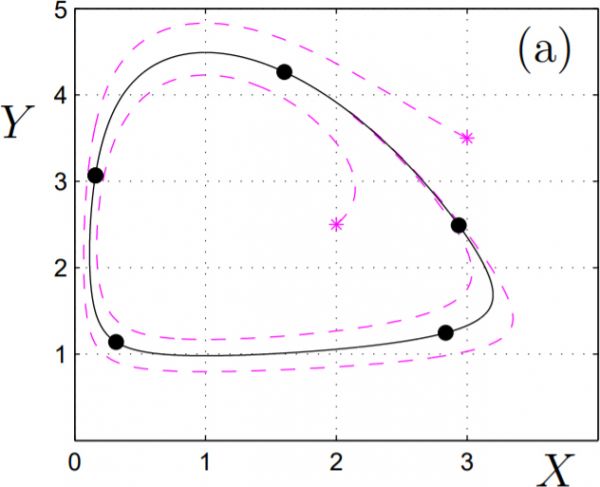
Figure 1: Dynamics in a specific example. (a) Stable periodic orbit \(γ(t)\) of (33) (solid black) and two other trajectories (dashed magenta) with initial conditions marked by stars; the parameters are given in (34). Five points (black dots) are shown on the limit cycle for orientation purposes which are equally space over one period.