barter2021closed
A closed form for Jacobian reconstruction from time series and its application as an early warning signal in network dynamics
Edmund Barter, Andreas Brechtel, Barbara Drossel and Thilo Gross
Proc. R. Soc. A. 477, 20200742, 2021
The Jacobian matrix of a dynamical system describes its response to perturbations. Conversely one can estimate the Jacobian matrix by carefully monitoring how the system responds to environmental noise. Here we present a closed form analytical solution for the calculation of a system's Jacobian from a timeseries. Being able to access a system's Jacobian enables us to perform a broad range of mathematical analyses by which deeper insights into the system can be gained. Here we consider in particular the computation of the leading Jacobian eigenvalue as an early warning signal for critical transition. To illustrate this approach we apply it to ecological meta-foodweb models, which are strongly nonlinear dynamical multi-layer networks. Our analysis shows that accurate results can be obtained, although the data demand of the method is still high.
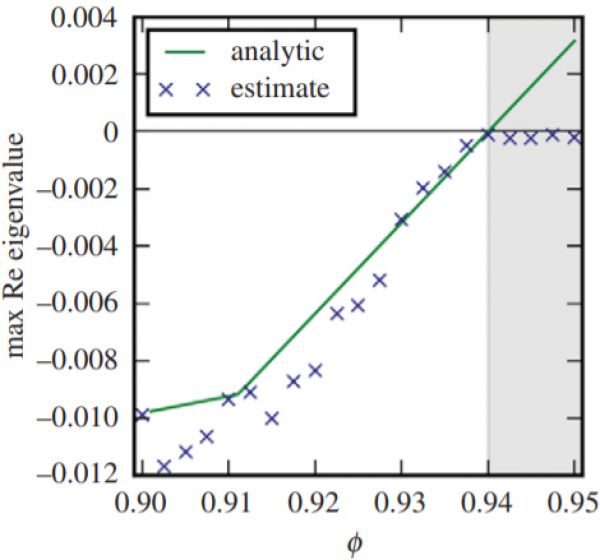
Figure 1: Jacobian eigenvalue reconstructed from correlations in simulated measurements in a large meta-foodweb (symbols) in comparison to the analytical ground truth (line).