BioND | Fragmentation transitions in multistate voter models

Abstract Citation export ArXiv preprint Publisher's page

bohme2012fragmentation

Fragmentation transitions in multistate voter models

Gesa A. Böhme and Thilo Gross

Phys. Rev. E 85, 066117, 2012

Adaptive models of opinion formation among humans can display a fragmentation transition, where a social network breaks into disconnected components. Here, we investigate this transition in a class of models with arbitrary number of opinions. In contrast to previous work we do not assume that opinions are equidistant or arranged on a one-dimensional conceptual axis. Our investigation reveals detailed analytical results on fragmentations in a three-opinion model, which are confirmed by agent-based simulations. Furthermore, we show that in certain models the number of opinions can be reduced without affecting the fragmentation points.

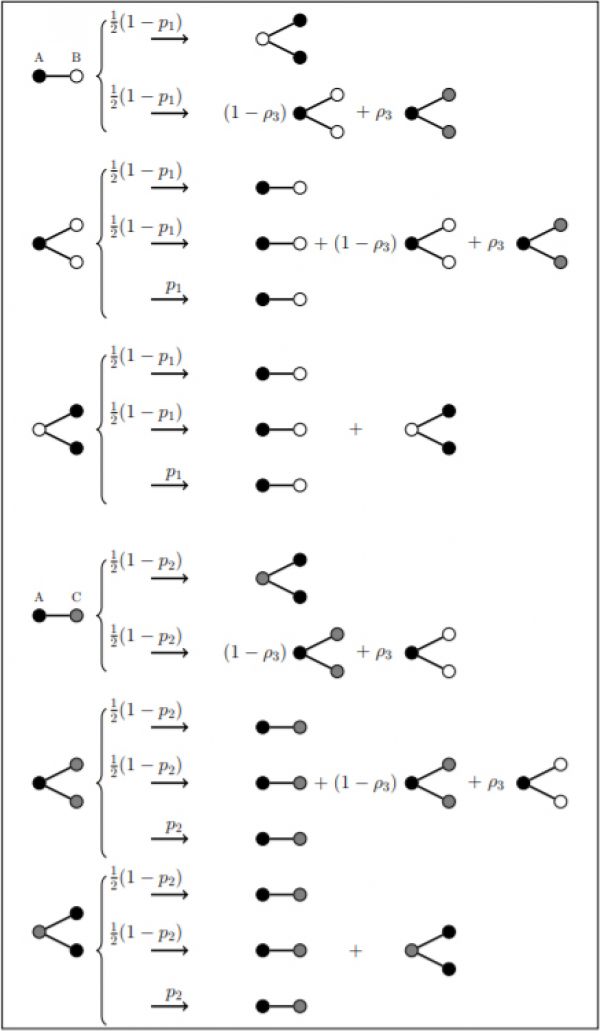
$Transitions of AB- and AC-fans for a degree-regular network with $k = 3$ and equiprobable states for the scenario of partial fragmentation with respect to A. Black, white and grey nodes correspond to agents holding opinion A, B, and C, respectively. The active link densities $ρ_1$ and $ρ_2$ are assumed to vanish close to the partial fragmentation point, whereas $ρ_3$, the densitiy of BC-links can be finite.$

Figure 1: Transitions of AB- and AC-fans for a degree-regular network with $k = 3$ and equiprobable states for the scenario of partial fragmentation with respect to A. Black, white and grey nodes correspond to agents holding opinion A, B, and C, respectively. The active link densities $ρ_1$ and $ρ_2$ are assumed to vanish close to the partial fragmentation point, whereas $ρ_3$, the densitiy of BC-links can be finite.