gross2004analytical
Analytical search for bifurcation surfaces in parameter space
Thilo Gross and Ulrike Feudel
Physica D: Nonlinear Phenomena 195, 292-302, 2004
The method of resultants can be used to compute Hopf bifurcations in ODE systems. We discuss this method from the applicant’s point of view. Furthermore, we show by theory and examples that the method may be extended to cover other bifurcation situations as well. Among them are the real Hopf situation, which plays an important role in the transition to Shil’nikov chaos as well as some higher codimension bifurcations, such as Takens–Bogdanov, Gavrilov–Guckenheimer, and double Hopf bifurcations. The method yields an analytical test function that can be solved analytically or by computer algebra systems. In contrast to common analytical techniques based on eigenvalue computation (which can only be applied to systems of size \(N\leq 4\)), the method is applicable for systems of intermediate size (\(N<10\)). We illustrate the power of the method by discussing examples from different disciplines of science: a Lorenz-like oscillator, two coupled oscillators, and a five-species food chain.
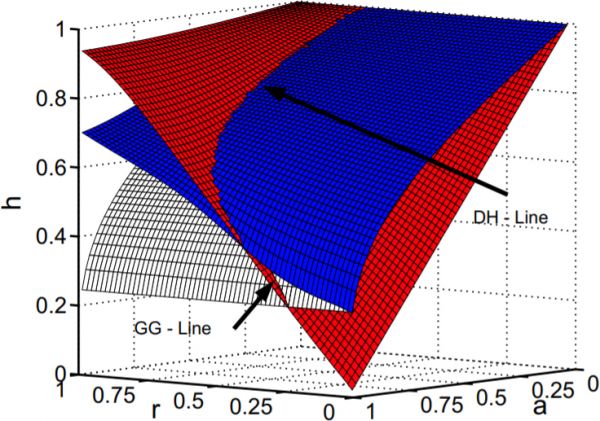
Figure 1: Bifurcations of the 5-level foodchain. The two dark surfaces correspond to Hopf bifurcations while the white surface will in general be a transcritical bifurcation. A double Hopf (DH) bifurcation line is formed at the intersection of the dark
surfaces. Furthermore there is a Gavrilov-Guckenheimer (GG) bifurcation line at the intersection of one of the dark surfaces with the white surface.