gross2008robust
Robust oscillations in SIS epidemics on adaptive networks: Coarse-graining by automated moment closure
We investigate the dynamics of an epidemiological susceptible-infected-susceptible (SIS) model on an adaptive network. This model combines epidemic spreading (dynamics on the network) with rewiring of network connections (topological evolution of the network). We propose and implement a computational approach that enables us to study the dynamics of the network directly on an emergent, coarse-grained level. The approach sidesteps the derivation of closed low-dimensional approximations. Our investigations reveal that global coupling, which enters through the awareness of the population to the disease, can result in robust large-amplitude oscillations of the state and topology of the network.
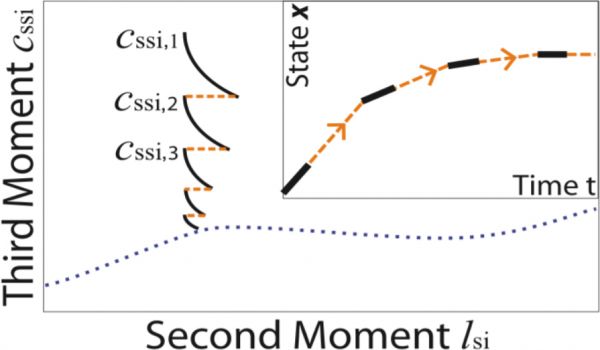
Figure 1: Schematic of the lifting procedure. A network with initially arbitrary third moments is settled to the slow manifold (dotted line) on which the consistent values encountered in the long-term dynamics are located. For this purpose we run a short simulation (solid line) and then reset the first and second moments while retaining the third moments (dashed line). Inset: Illustration of coarse projective integration. The necessary information for long projective
leaps (dashed) is extracted from short bursts of individual-based simulation (solid).