hesse2014selforganized
Self-organized criticality as a fundamental property of neural systems
Janina Hesse and Thilo Gross
Front. Syst. Neurosci. 8, 166, 2014
The neural criticality hypothesis states that the brain may be poised in a critical state at a boundary between different types of dynamics. Theoretical and experimental studies show that critical systems often exhibit optimal computational properties, suggesting the possibility that criticality has been evolutionarily selected as a useful trait for our nervous system. Evidence for criticality has been found in cell cultures, brain slices, and anesthetized animals. Yet, inconsistent results were reported for recordings in awake animals and humans, and current results point to open questions about the exact nature and mechanism of criticality, as well as its functional role. Therefore, the criticality hypothesis has remained a controversial proposition. Here, we provide an account of the mathematical and physical foundations of criticality. In the light of this conceptual framework, we then review and discuss recent experimental studies with the aim of identifying important next steps to be taken and connections to other fields that should be explored.
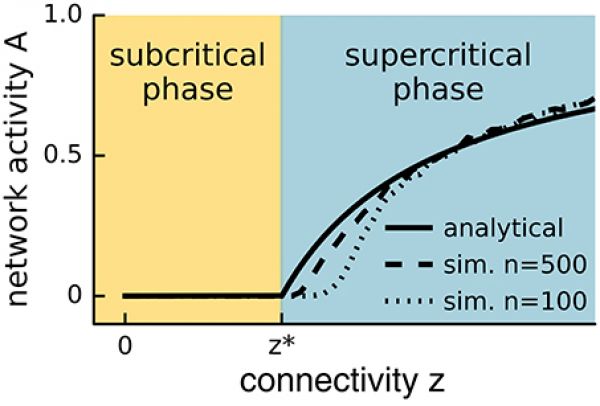
Figure 1: Network activity versus connectivity for the steady state solution of Equation (1) (straight line) and a simulated network with \(n = 500\) (dashed line) or \(n = 100\) (lower dashed line) neurons. A phase transition is observed at \(z^*\) (see main text) for the analytical solution with infinite n, whereas the transition appears in finite systems at slightly higher values of the control parameter and is smoothed out over a small interval. In the event-based simulation of Equation (1), the steady state network activity \(A\) was measured as \(A = s\tau /\eta T\), where s is the number of spikes recorded during the time period T following an initial relaxation period \(\eta\), and \(\tau\) is the period over which the neuron remains active.