hofener2013amplitude
Amplitude death in networks of delay-coupled delay oscillators
Johannes M. Höfener, Gautam C. Sethia and Thilo Gross
Phil. Trans. R. Soc. A. 371, 20120462, 2013
Amplitude death is a dynamical phenomenon in which a network of oscillators settles to a stable state as a result of coupling. Here, we study amplitude death in a generalized model of delay-coupled delay oscillators. We derive analytical results for degree homogeneous networks which show that amplitude death is governed by certain eigenvalues of the network’s adjacency matrix. In particular, these results demonstrate that in delay-coupled delay oscillators amplitude death can occur for arbitrarily large coupling strength \(k\). In this limit, we find a region of amplitude death which already occurs at small coupling delays that scale with \(1/k\). We show numerically that these results remain valid in random networks with heterogeneous degree distribution.
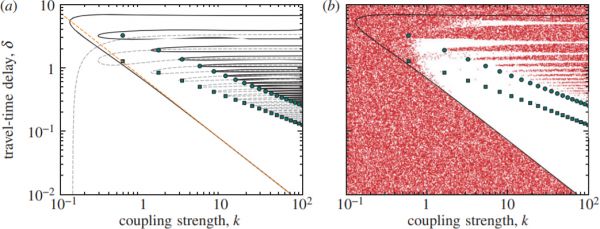
Figure 1: Amplitude death for large coupling strength. (a) Bifurcation lines from the eigenvalue \(c = d\) (solid lines) and \(c =−d\) (dashed lines). The approximate tip positions of tongues have been marked by circles (\(c = d\)) and squares (\(c = −d\)). The diagonal dashed line marks the analytical approximation to the bottom boundary of the stable region. For sufficiently largek, all DHONs are stable between this bifurcation line and the tongues corresponding to \(c = −d\). Non-bipartite networks are even stable up the tongues corresponding to \(c = d\). (b) Numerical results from uniform sampling of the space shown for random networks with \(N = 10\) nodes and \(K = 15\) edges. Dots mark unstable parameter points such that the large white regions mark stable areas that correspond to amplitude death. In particular, for sufficiently large \(k\), no unstable networks are found for \(\delta\) between the bottom bifurcation line with (\(d = 2K/N\)) and the tip positions for \(c = −d\). Most networks are stable up to the tip positions for \(c = d\). In the double logarithmic plot, the region of amplitude death grows with increasing k as its boundaries approach power lawswith exponent \(−1\) and \(−1/2\), respectively, in agreement with analytical predictions.