BioND | Branching process in a stochastic extremal model

Download PDF Abstract Citation export ArXiv preprint Publisher's page

manna2009branching

Branching process in a stochastic extremal model

S. S. Manna

Phys. Rev. E 80, 021132, 2009

We considered a stochastic version of the Bak-Sneppen model (SBSM) of ecological evolution where the the number $M$ of sites mutated in a mutation event is restricted to only two. Here the mutation zone consists of only one site and this site is randomly selected from the neighboring sites at every mutation event in an annealed fashion. The critical behavior of the SBSM is found to be the same as the BS model in dimensions $d =1$ and $2$. However on the scale-free graphs the critical fitness value is non-zero even in the thermodynamic limit but the critical behavior is mean-field like. Finally $\langle M\rangle$ has been made even smaller than two by probabilistically updating the mutation zone which also shows the original BS model behavior. We conjecture that a SBSM on any arbitrary graph with any small branching factor greater than unity will lead to a self-organized critical state.

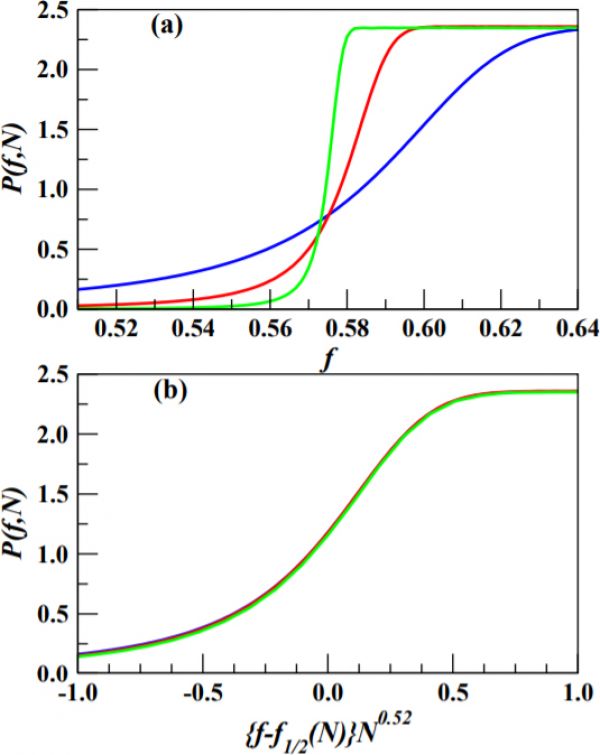
$The distributions $P(f, N)$ of the fitness values in the steady state of SBSM on the Barabasi-Albert scale-free graph. (a) Distribution plots for the graph sizes $N = 2^7$ (blue), $2^{10}$ (red) and $2^{13}$ (green). The jump in the distribution becomes gradually sharper with increasing the system sizes. (b) A finite-size scaling of this data shows an excellent collapse.$

Figure 1: The distributions $P(f, N)$ of the fitness values in the steady state of SBSM on the Barabasi-Albert scale-free graph. (a) Distribution plots for the graph sizes $N = 2^7$ (blue), $2^{10}$ (red) and $2^{13}$ (green). The jump in the distribution becomes gradually sharper with increasing the system sizes. (b) A finite-size scaling of this data shows an excellent collapse.