BioND | Mesoscopic structures and the Laplacian spectra of random geometric graphs

Abstract Citation export ArXiv preprint Publisher's page

nyberg2015mesoscopic

Mesoscopic structures and the Laplacian spectra of random geometric graphs

Amy Nyberg, Thilo Gross and Kevin E. Bassler

J. Comp. Networks 3, 543-551, 2015

We investigate the Laplacian spectra of random geometric graphs (RGGs). The spectra are found to consist of both a discrete and a continuous part. The discrete part is a collection of Dirac delta peaks at integer values roughly centered around the mean degree. The peaks are mainly due to the existence of mesoscopic structures that occur far more abundantly in RGGs than in non-spatial networks. The probability of certain mesoscopic structures is analytically calculated for one-dimensional RGGs and they are shown to produce integer-valued eigenvalues that comprise a significant fraction of the spectrum, even in the large network limit. A phenomenon reminiscent of Bose-Einstein condensation in the appearance of zero eigenvalues is also found.

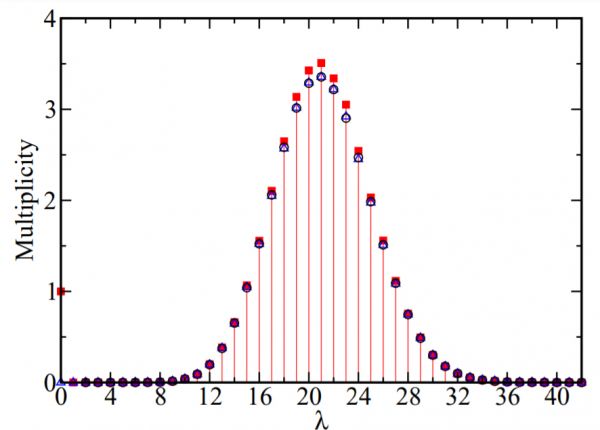
$Ensemble-averaged integer eigenvalue multiplicity for 1d RGGs with $N = 100$ and $r = 0.1$. The red points are the results of numerical diagonalization of $10^6$ random ensemble realizations and the black points are the number due to Type-I orbits according to Eq. 1.$

Figure 1: Ensemble-averaged integer eigenvalue multiplicity for 1d RGGs with $N = 100$ and $r = 0.1$. The red points are the results of numerical diagonalization of $10^6$ random ensemble realizations and the black points are the number due to Type-I orbits according to Eq. 1.