BioND | Consensus time and conformity in the adaptive voter model

Abstract Citation export ArXiv preprint Publisher's page

rogers2013consensus

Consensus time and conformity in the adaptive voter model

Tim Rogers and Thilo Gross

Phys. Rev. E 88, 030102, 2013

The adaptive voter model is a paradigmatic model in the study of opinion formation. Here we propose an extension for this model, in which conflicts are resolved by obtaining another opinion, and analytically study the time required for consensus to emerge. Our results shed light on the rich phenomenology of both the original and extended adaptive voter models, including a dynamical phase transition in the scaling behavior of the mean time to consensus.

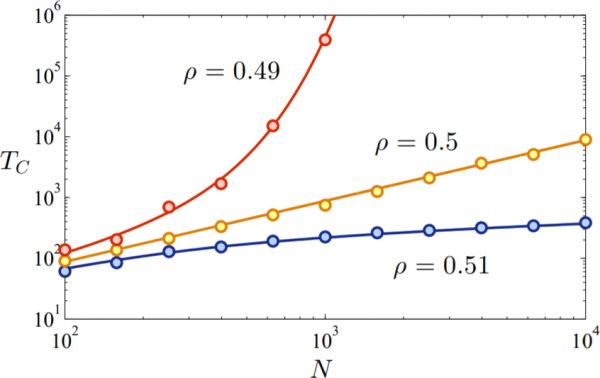
$Dynamical phase transition in the scaling behavior of the mean time to reach consensus TC as a function of network size $N$. At the critical value $\rho = 1/2$ the growth of TC is linear, whilst being exponential for ρ above the critical point, and logarithmic below. In each case circles give the average over 100 simulation runs with $k = 10$ and $\phi = 0.1$, while the solid lines show the result of the theory developed in the main text – see equation (7).$

Figure 1: Dynamical phase transition in the scaling behavior of the mean time to reach consensus TC as a function of network size $N$. At the critical value $\rho = 1/2$ the growth of TC is linear, whilst being exponential for ρ above the critical point, and logarithmic below. In each case circles give the average over 100 simulation runs with $k = 10$ and $\phi = 0.1$, while the solid lines show the result of the theory developed in the main text – see equation (7).