yeakel2018ecoevolutionary
Eco-evolutionary dynamics, density-dependent dispersal and collective behaviour: implications for salmon metapopulation robustness
Justin D. Yeakel, Jean P. Gibert, Thilo Gross, Peter A. H. Westley and Jonathan W. Moore
Phil. Trans. R. Soc. B 373, 20170018, 2018
The spatial dispersal of individuals is known to play an important role in the dynamics of populations, and is central to metapopulation theory. At the same time, local adaptation to environmental conditions creates a geographic mosaic of evolutionary forces, where the combined drivers of selection and gene flow interact. Although the dispersal of individuals from donor to recipient populations provides connections within the metapopulation, promoting demographic and evolutionary rescue, it may also introduce maladapted individuals into habitats host to different environmental conditions, potentially lowering the fitness of the recipient population. Here we explore a model of the eco-evolutionary dynamics between two populations connected by dispersal, where the productivity of each is defined by a trait complex that is subject to local selection. Although general in nature, our model is inspired by salmon metapopulations, where dispersal between populations is defined in terms of the straying rate, which has been shown to be density-dependent. The results of our model reveal that increased straying between evolving populations leads to alternative stable states, which has large and nonlinear effects on two measures of metapopulation robustness: the portfolio effect and the time to recovery following an induced disturbance. We show that intermediate levels of straying result in large gains in robustness, and that increased habitat heterogeneity promotes robustness when straying rates are low, and erodes robustness when straying rates are high. Finally, we show that density-dependent straying promotes robustness, particularly when the aggregate biomass is low and straying is correspondingly high, which has important ramifications for the conservation of salmon metapopulations facing both natural and anthropogenic disturbances.
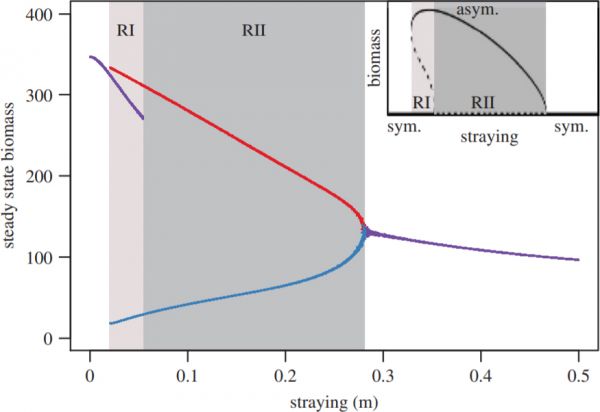
Figure 1: The steady-state densities of \(N_i\) and \(N_j\) versus straying m for the constant straying model. Alternative stable states exist for regimes I and II, labelled RI and RII, respectively. In regime I, the system can approach qualitatively different states: a symmetric, intermediate state ( purple), and asymmetric dominant (red) and subordinate (blue) states. In regime II, only one type of attractor exists: an asymmetric dominant/subordinate state (red and blue points, respectively), and its mirror image where identities of dominant and subordinate are exchanged. Inset: a qualitative sketch of the bifurcation diagram, showing the stable (solid lines) and unstable (dashed lines) fixed points in regimes I (light grey area) and II (dark grey area). The symmetric condition (sym.) is the horizontal line at the base of the inset, whereas the asymmetric condition (asym.) is represented by the curved line.