zschaler2012early
Early fragmentation in the adaptive voter model on directed networks
Gerd Zschaler, Gesa A. Böhme, Michael Seißinger, Cristián Huepe and Thilo Gross
Phys. Rev. E 85, 046107, 2012
We consider voter dynamics on a directed adaptive network with fixed out-degree distribution. A transition between an active phase and a fragmented phase is observed. This transition is similar to the undirected case if the networks are sufficiently dense and have a narrow out-degree distribution. However, if a significant number of nodes with low out degree is present, then fragmentation can occur even far below the estimated critical point due to the formation of self-stabilizing structures that nucleate fragmentation. This process may be relevant for fragmentation in current political opinion formation processes.
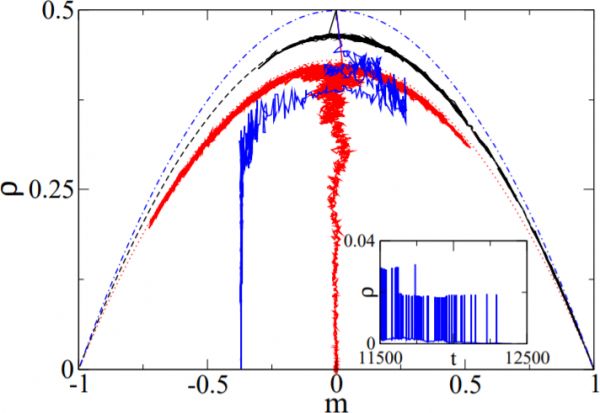
Figure 1: Typical trajectories from network simulations. The state of the network is characterized by the density of active links \(\rho\) and the magnetization \(m\). The trajectories shown correspond to networks with Poissonian out-degree distributions with \(\langle k \rangle = 4 \) (red/light gray), \( \langle k\rangle = 8 \) (black), and an out-degree distribution following \( P_{\rm out\}(k) \sim k^{-2} \) (blue/dark gray). The trajectories initially drift along a parabola of active states (dotted red, dashed black, and dash-dotted blue lines, denoting analytical results from Eq. (10)). However, only the black trajectory reaches a consensus state, whereas the others eventually collapse to a fragmented state.
The inset shows a time series of ρ from the scale-free network shortlybefore fragmentation.
