fahimipour2021sharp
Sharp thresholds limit the benefit of defector avoidance in cooperation on networks
Ashkaan K. Fahimipour, Fanqi Zeng, Martin Homer, Arne Traulsen, Simon A. Levin and Thilo Gross
PNAS 119, e2120120119, 2022
Consider a cooperation game on a spatial network of habitat patches, where players can relocate between habitats if they judge the local conditions to be unfavorable. In time, the relocation events may lead to a homogeneous state where all patches harbor the same densities of cooperators and defectors or they may lead to self-organized patterns, where some patches become safe havens that maintain a high cooperator density. Here we analyze the transition between these states mathematically. We show that safe havens form once a certain threshold in connectivity is crossed. This threshold can be analytically linked to the structure of the patch network and specifically to certain network motifs. Surprisingly, a forgiving defector-avoidance strategy may be most favorable for cooperators. Our results demonstrate that the analysis of cooperation games in ecologically-inspired metacommunity models is mathematically tractable and has the potential to link diverse topics such as macroecological patterns, behavioral evolution, and network topology.
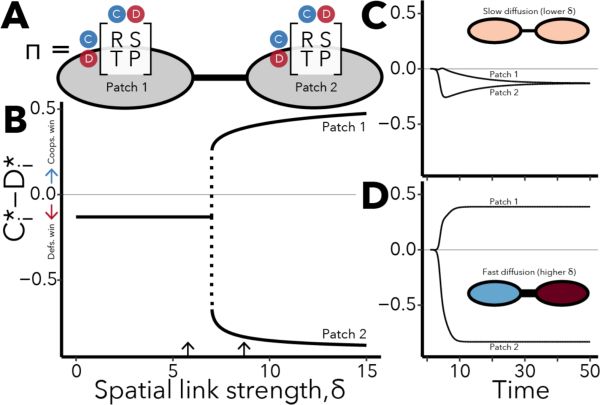
Figure 1: Emergence of a heterogeneous stationary state on a 2-patch network. A. Schematic of the spatial
game, showing local payoff relationships among cooperators and defectors occupying the same patch (gray
circles) and the dispersal route between them. B. Difference in equilibrium densities of both types in patches
1 and 2 as link strength is varied. Arrows refer to the example time series shown in panels C and D. C. The
homogeneous steady state, with identical equilibrium densities of C and D across locations. The inset network
shows whether cooperators or defectors dominate each patch (darker blues or reds, respectively). D. The same
game, but with faster diffusion on the network, showing emergence of a heterogeneous steady state with high
cooperator densities in patch 1.