gross2005long
Long food chains are in general chaotic
Thilo Gross, Wolfgang Ebenhöh and Ulrike Feudel
Oikos 109, 135-144, 2005
The question whether chaos exists in nature is much debated. In this paper we prove that chaotic parameter regions exist generically in food chains of length greater than three. While nonchaotic dynamics is also possible, the presence of chaotic parameter regions indicates that chaotic dynamics is likely. We show that the chaotic regions survive even at high exponents of closure. Our results have been obtained using a general food chain model that describes a large class of different food chains. The existence of chaos in models of such generality can be deduced from the presence of certain bifurcations of higher codimension.
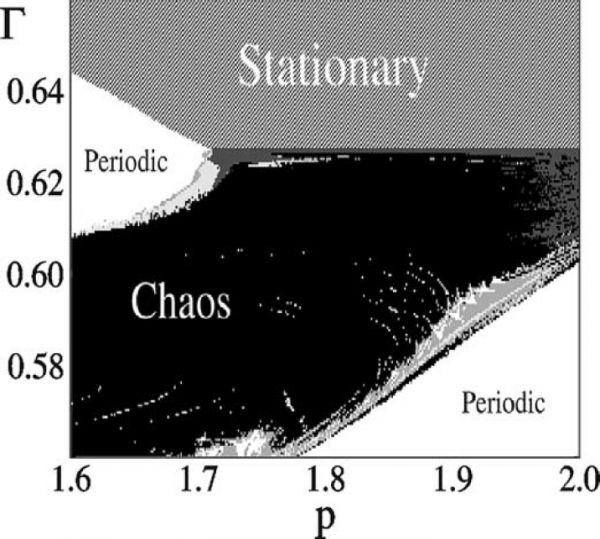
Figure 1: Qualitative behavior of a specific four-trophic food chain, depending on the exponent of closure \(p\) and the
sensitivity to prey density \(\Gamma\). Results are from the numerical computation of Lyapunov exponents. The attractor is a steady state (pattern), a limit cycle (white), a two-torus (medium grey), a three-torus (light grey) or a chaotic attractor (black). In the dark grey region all Lyapunov exponents are small. In this region the nature of the attractor could not be determined.