do2012graphical
Graphical notation reveals topological stability criteria for collective dynamics in complex networks
Anne-Ly Do, Stefano Boccaletti and Thilo Gross
Phys. Rev. Lett. 108, 194102, 2012
We propose a graphical notation by which certain spectral properties of complex systems can be rewritten concisely and interpreted topologically. Applying this notation to analyze the stability of a class of networks of coupled dynamical units, we reveal stability criteria on all scales. In particular, we show that in systems such as the Kuramoto model the Coates graph of the Jacobian matrix must contain a spanning tree of positive elements for the system to be locally stable.
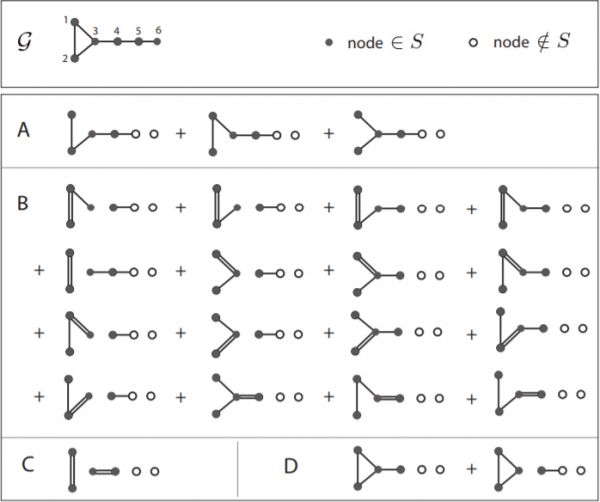
Figure 1: Symbolic calculation of a determinant using the graphical notation. We can immediately read off that \(D_{4,S} ≡ A = \Phi_S\), defined in the text.