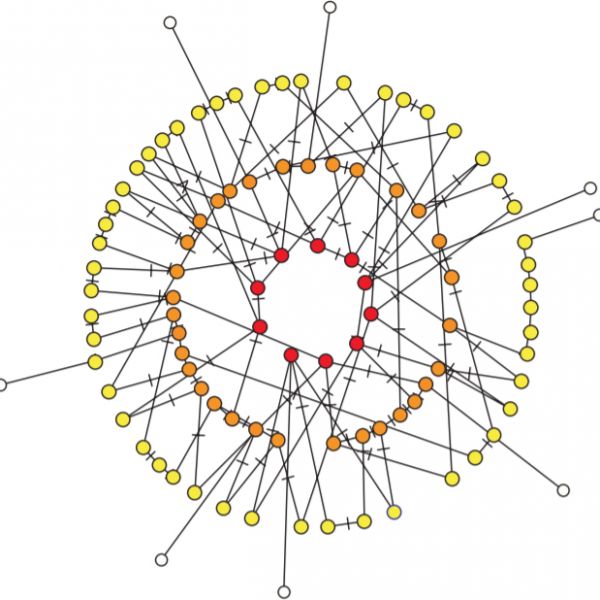
Adaptive Networks
In an adaptive network the network structure responds dynamically to the state of the nodes, while the nodes are subject to processes that occur on that structure.
A simple example is an epidemic where infected people self-isolate to avoid infecting their friends . The infection is transmitted along the links of the network, hence it is a structure-dependent process that affects node states. The self-isolation of infected breaks links in the network and hence is a node-dependent process that affects the structure. In this way a dynamical feedback loop between the state and the topology is formed that gives adaptive networks the ability to self-organize in interesting and often unexpected ways.
Generalized Models
Generalized models are models in which one specifies the structure of interactions in a system but does not restrict the interactions to a particular functional form. Hence one generalized model can describe a family of different models. This is particularly useful for modelling systems on which we have limited information as the generalized model can capture the full range of potential relationships that might be realized in nature. Despite their generality, generalized models can be studied highly efficiently and often yield deep insights into the functioning of a system.
Generalized models have existed for a long time. Since the beginnings of modelling, some statements have been made over models that contain unspecified functions. In a sense all of bifurcation theory focusses on dynamical systems of the general form \(\dot{x}=f(x)\). However, in a narrow sense generalized models refer to a class of general equation systems that are parameterized using one particular trick .
Diffusion Maps
The 21st century is characterized by rise of massive data sets that are not only large because of sheer size but also complex due to the breadth of information they capture. Many well-established data analysis methods fail in these novel datasets due to the so-called curse of dimensionality. Diffusion maps, a method proposed by Coifman et al. is a powerful tool to reduce this dimensionality by identifying the the most important dimensions in a system, which emerge as nonlinear functions of the primary data.
In contrast to linear methods such as principal component analysis (PCA), the diffusion map is a fully nonlinear method. In contrast to many other methods that are superficially similar (e.g. neighborhood embeddings) the diffusion map focusses on capturing the large-scale structure of datasets. It profits from a strong physical intuition and is fully deterministic and (in our formulation) almost parameter-free.