BioND | Adaptive Networks

Adaptive Networks

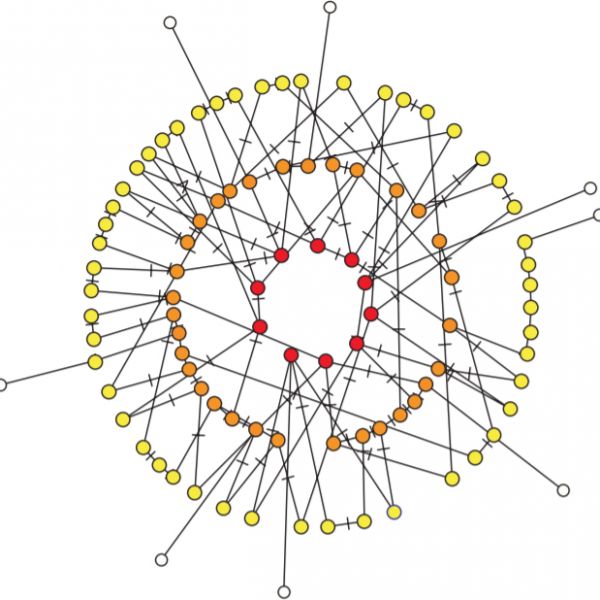
In an adaptive network the network structure responds dynamically to the state of the nodes, while the nodes are subject to processes that occur on that structure.

A simple example is an epidemic where infected people self-isolate to avoid infecting their friends [1]. The infection is transmitted along the links of the network, hence it is a structure-dependent process that affects node states. The self-isolation of infected breaks links in the network and hence is a node-dependent process that affects the structure. In this way a dynamical feedback loop between the state and the topology is formed that gives adaptive networks the ability to self-organize in interesting and often unexpected ways.

A brief history

In certain applications adaptive networks have already for a long time. However, the realization that the state-structure feedback gives rise to a distinct set of phenomena only dawned in response to four ground-breaking papers in 2000. These include the neural model of Bornholdt and Rohlf [2], an abstract Boolean network by Paczuski et al. [3], a network formation model by Skyrms and Pemantle [4], and network cooperation game by Zimmermann et al. [5]. It followed a steady trickle of papers in a broad variety of applications.

Adaptive networks really took of with an explosion of papers in 2006. In this year also our own first contribution to adaptive networks [1] was published. In this paper we showed how properties of the network structure can act as variables in epidemic dynamics. Later it would be shown by Scarpino et al. [6] with a closely-related that the resulting feedback explained a previously unexplained phenomenon in epidemic data.

Our 2006 paper [1] also led to the widespread adoption of the name 'adaptive networks' and the subsequent review [7] contributed to their recognition as an independent class of networks within network science.

Interplay of topology and local states

What makes adaptive networks interesting is the dynamical interplay between network topology and local node states. Dynamics on a static network are often effectively low dimensional which limits the range of dynamical phenomena that can be observed. By contrast, in an adaptive network the dynamics of the nodes reshape the topology. The myriad of topological degrees of freedom then act as a memory leading to complex and often surprising dynamics.

Among the dynamical phenomena that have been observed in adaptive networks is the robust self-organization to critical state, the emergence of phase transitions involving structural and dynamical variables, and the emergence of complex self-organized structures from homogeneous initial conditions.

Mathematical investigation

Most adaptive networks models consider discrete-state notes (e.g. infected and susceptible agents). These models can be explored mathematically using network moment expansions, which were first applied to adaptive networks in [1].

While moment expansions continue to be the main workhorse for adaptive networks studies, there are some systems that can only be poorly described with this type of approximation, particularly these are systems that can undergo fragmentation transitions, where the networks breaks into multiple components. A classic example, proposed originally by Holme and Newman [8] and analyzed in details by Vazquez et al. [9]. BioND lab managed to show this type of system much can be much more accurately described by a different type of approximation that we call motif expansion [10].

Among other mathematical ideas that the lab has pioneered is the so-called triple jump method [11] in which one uses a very accurate type of moment expansion that leads to an infinite dimensional differential equation system. Due to their particular structure these systems can then be mapped exactly to a two-dimensional partial differential equation in two-dimensional space. If this equation is hyperbolic it can further be mapped back onto a low-dimensional ordinary differential equation, which can then be solved.

While there is no universal approximation that works well for every adaptive networks, we have discovered some general approaches that allow us to build approximation schemes that work for a particular application. For example we were thus able to analyze a very difficult growing adaptive network, that approximates scale-free degree distributions [12].

A subject we are particularly fascinated with is the analysis of continuous valued adaptive networks. Although the high dimensional dynamics make this class of systems particularly tricky, they lend themselves to application of elegant methods from algebra and exhibit surprising types of self-organization [13,14].

Applications

Adaptive networks have been widely applied but at least for this lab four applications stand out in particular. Perhaps the premier application of adaptive networks are epidemic dynamics. Our paper in this area [1] inspired many many subsequent works, which used adaptive networks to model social distancing responses to epidemic states of agents. Some of our own subsequent contributions to this field are [12], which showed that adaptive behavior leads can lead to vanishing epidemic thresholds in networks where the degree distribution has a finite second moment, and [15] which showed that a small transient epidemic can leave networks "inocculated" against a subsequent epidemic even if the individual nodes do not retain resistance against the disease.

Another application that is currently getting a lot of attention is neural criticality. Our brains seem to be poised at a transition between two different dynamical regimes. The adaptive self-organization of synapses may explain why the brain manages to stay exactly on this narrow edge on which meaningful information processing is possible. Building on the pioneering work of Bornholdt and Rohlf [2] we formulated the first fairly realistic model of neural self-organization [16] and demonstrated some prediction in data from patients [17]. However, the main focus of the lab has been to explore the underlying dynamical foundations of adaptive self-organization [18,19,20].

Perhaps the biggest problem of our time is the post-truth phenomenon. Here adaptive networks can be used to understand social self-organization processes that lead to the formation to echo chambers. The foundational adaptive network model in this area is the voter model [8,9]. Our main contribution in this area is to demonstrate that a variant of this model describes collective motion in animals [21,22] this contributed to the discovery of new phenomenon that demonstrated in experiments [23].

Apart form the specific application of misinformation there is a wider interest in the adaptive self-organization of social interactions. In particular we used adaptive networks to study the evolution of cooperative behavior and the formation of cooperation networks in common goods games. Among others we showed that a dynamical instability can lead to cooperative behavior in a discrete state model of cooperation [24]. In continuous state models an even richer phenomenology of self-organization emerges where some nodes rise to leadership position due to spontaneous pattern formation [13].